Freya's Blog - New Morning

用matlab软件实现Kolmogorov-Smirnov检验

K-S检验是来自某一特定分布的方法。它的检验方法是以样本数据的经验分布函数与特定理论分布比较，若两者间的差距很小，则推论该样本取自某特定分布族。

即对于假设检验问题：

H=0：样本所来自的总体分布服从某特定分布；

H=1：样本所来自的总体分布不服从特定分布。

k-s检验的检验统计量是

$$max(|F_n(x)-F(x)|)$$

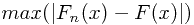
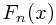
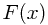其中， $$F_n(x)$$ 是经验分布函数， $F(x)$ 是理论分布函数。

经验分布函数：

设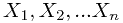 $X_1,X_2,...X_n$ 是抽自总体X的一个样本，观察值为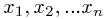,次序观测值为 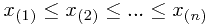${x_{(1)}}\le{x_{(2)}}\le...\le{x_{(n)}}$ ，则总体X的经验分布函数定义为

$F_n(x)=\frac{Observed~values~no.~which~is~smaller~than~x~in~sample}{n},\forall{x}\in{R}.$

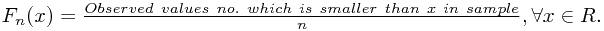
即

$F_n(x)=\begin{cases}0&x\leq{x_{(1)}}\cr\frac{k}{n}&x_{(k)}\le{x}\leq{x_{(k+1)}},k=1,...,n-1\\1&x>{x_{(n)}}$

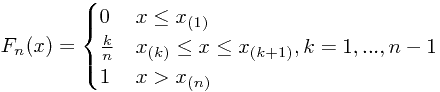
理论分布函数：

由于我们产生的是服从0-1均匀分布的随机数，(a,b)均匀分布的分布函数为

$F(x)=\begin{cases}0&x<a\cr\frac{x-a}{b-a}&a\leq{x}<b\\1&x\geq{b}$

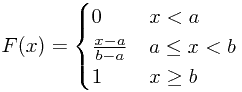
将a=0，b=1代入公式，可得到数据的理论分布函数。

matlab代码如下：

path=strcat(pwd,'\filename');
x=importdata(path);
x=sort(x);
                 
%画出经验分布函数
figure
cdfplot(x);
hold on
%画出标准分布函数
plot(x,unifcdf(x,0,1),'r-');
hold off
    
%检验数据序列符合均匀分布的程度
[H,pvalue]=kstest(x[x,unifcdf(x,0,1)],0.05);